二叉树主题

2023-08-06

遍历

关于二叉树遍历有很多有趣的主题，比如BST的中序遍历是一个有序序列。我们可能还想知道如何进行层次遍历（使用队列），这是进行广度优先搜索（BFS）的基础。在下面的每个部分中，我们将讨论这些主题。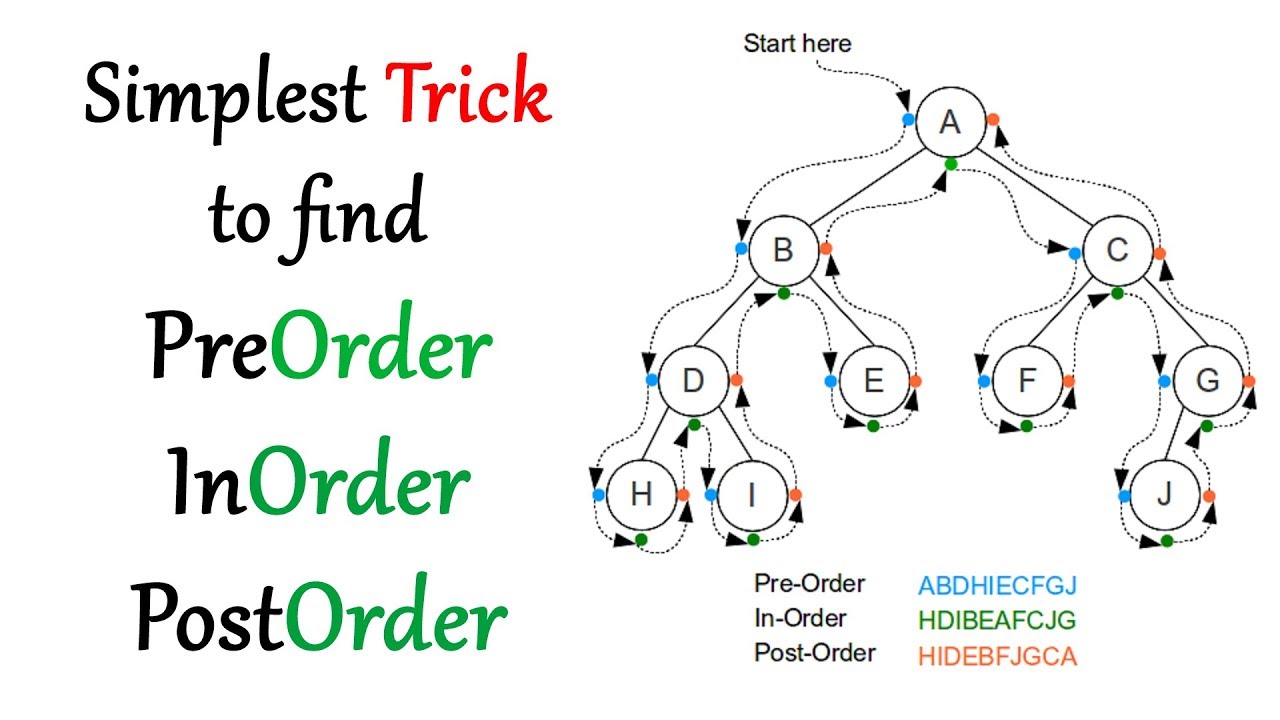
traverse

前序遍历

前序遍历将按照根节点 -> 左子节点 -> 右子节点的顺序访问。

中序遍历

中序遍历将按照左子节点 -> 根节点 -> 右子节点的顺序访问。BST的中序遍历将返回一个有序数组。

后序遍历

后序遍历将按照左子节点 -> 右子节点 -> 根节点的顺序访问。

要确定一棵二叉树，我们需要中序序列 + 前序/后序序列。

解决二叉树问题的方法论

一个重要的观察是，当我们查看根节点的位置时，从前序到后序，它从第一个变为最后一个。由于我们总是在访问右子节点之前访问左子节点，我们可以将不同遍历之间的差异仅视为何时对根节点进行操作。

然后我们可以将问题归纳为几种情况：

  1. 要对根节点进行操作，你需要先对左子树和右子树进行操作。（归并排序）
  2. 要对根节点进行操作，你需要先对其父节点进行操作。（获取二叉树的深度）
  3. 要对根节点进行操作，你需要先对左/右子树进行操作。（检查BST）

上述三种情况大致涵盖了所有三种遍历方法。给定一个问题，我们需要注意对给定节点的操作是什么，以及何时进行操作。前序、中序还是后序？

二叉搜索树（BST）是一种特殊的二叉树，对于给定的根节点，左子树只包含值小于根节点的节点，右子树只包含值大于根节点的节点。

经典主题/问题

以下是一些你可能想了解的著名主题和问题。

最低公共祖先

最低公共祖先问题是尝试获取两个给定节点的最低公共祖先节点。

1
2
3
4
5
6
7
8
9
TreeNode lowestCommonAncestor(TreeNode root, TreeNoe t1, TreeNode t2) {
    if(root == null || root == t1 || root == t2) return root;
    TreeNode l = lowestCommonAncestor(root.left, t1, t2);
    TreeNode r = lowestCommonAncestor(root.right, t1, t2);
    if(l != null && r != null) return root;
    else if(l != null) return l;
    else if(r != null) return r;
    else return null;
}

为了以适合上述3种情况的方式分析解决方案，让我们思考一下我们需要对单个节点做什么操作。
基本上，我们需要遍历二叉树中的每个节点，以确定该节点是否是我们想要的LCA。对于给定节点，LCA可能是这个节点，但要确认这一点，我们需要确保两个目标节点都在它的子树中。这意味着除非我们完成检查它的左子树和右子树，否则我们无法确认这一点。这意味着它实际上是一个后序遍历。

二叉树的序列化和反序列化

从有序数组创建BST

从有序数组创建BST是另一个有趣的主题。

1
2
3
4
5
6
7
8
9
10
TreeNode buildBST(int[] array, int left, int right) {
    if(left == right) return new TreeNode(array[left]);
    int mid = (left + right) / 2;
    TreeNode left = buildBST(array, left, mid - 1);
    TreeNode right = buildBST(array, mid + 1, right);
    TreeNode root = new TreeNode(arr[mid]);
    root.left = left;
    root.right = right;
    return root;
}

可能的BST

给定一个有序数组，返回所有可能的BST。

BFS / 层序遍历

广度优先搜索/层序遍历尝试扫描每一层并打印值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void bfs(TreeNode root) {
    if(root == null) return;
    Queue<TreeNode> q = new LinkedList<>();
    q.offer(root);
    while(!q.isEmpty()) {
        int n = q.size();
        for(int i=0; i<n; i++) {
            TreeNode current = q.poll();
            System.out.print(current.val);
            if(current.left != null) q.offer(current.left);
            if(current.right != null) q.offer(current.right);
        }
        System.out.println(current.val);
    }
}

层序遍历可以被视为前序遍历的扩展变体。对于前序遍历，我们对单个根节点进行操作，然后移动到其左子节点和右子节点。但对于层次遍历，我们可以将同一层的节点视为一个节点，在我们完成对这个”大节点”的操作后，我们移动到它的子节点。